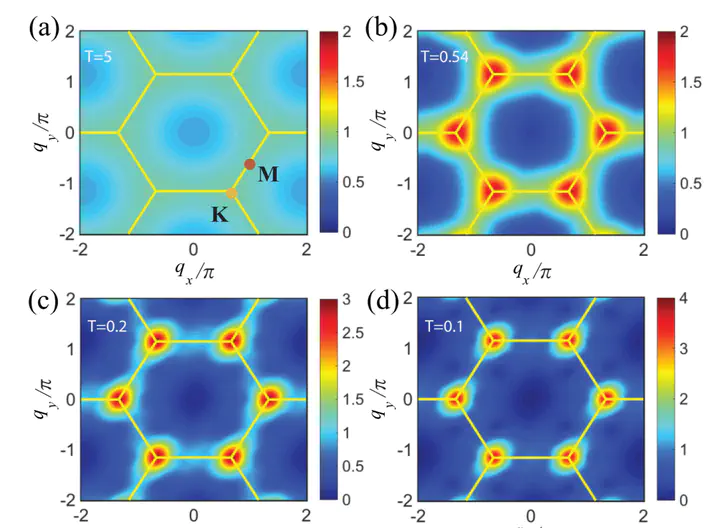
The anomalous thermodynamic properties of the paradigmatic frustrated spin-1/2 triangular-lattice Heisenberg antiferromagnet (TLH) has remained an open topic of research over decades, both experimentally and theoretically. Here, we further the theoretical understanding based on the recently developed, powerful exponential tensor renormalization group method on cylinders and stripes in a quasi-one-dimensional (1D) setup, as well as a tensor product operator approach directly in 2D. The observed thermal properties of the TLH are in excellent agreement with two recent experimental measurements on the virtually ideal TLH material Ba8CoNb6O24. Remarkably, our numerical simulations reveal two crossover temperature scales, at Tl/J$∼$0.20 and Th/J$∼$0.55, with J the Heisenberg exchange coupling, which are also confirmed by a more careful inspection of the experimental data. We propose that in the intermediate regime between the low-temperature scale Tl and the higher one Th, the ``rotonlike'' excitations are activated with a strong chiral component and a large contribution to thermal entropies. Bearing remarkable resemblance to the renowned roton thermodynamics in liquid helium, these gapped excitations suppress the incipient 120$∘$ order that emerges for temperatures below Tl.