第四章 晶格振动

Crystal Vibration

Atoms are in a perpetual movement in solids
“静止是相对的，运动是绝对的。“ ——运动是物质的存在方式与固有属性。哲学上说的运动是一般的、抽象的，但是马克思主义哲学的这个著名论断在描述晶格上发生的物理时，却是再合适不过了。

• 尽管晶体中的原子有序排列成近乎完美的晶格结构，但我们不能将其简单地视为静止的纯几何结构，而是要需要考虑其运动，才能理解固体的一些重要性质，如固体比热的低温反常、晶格的热输运、超导BCS理论等。

• 在热运动、外界扰动等影响下，晶格上的原子总是会在平衡位置附近运动，并形成一定的集体运动模式——晶格振动，并在系统中激发产生一种准粒子——声子。

• 场与准粒子

  • 量子化场的波动和准粒子激发可以联系起来。在理想的情况下，场的统计问题可以被简化成准粒子自由气体的统计问题。

  • 晶格振动与声子激发是一个多自由度的量子场论问题。我们也必须使用量子的理论才能够理解固体中晶格振动的性质。

  • ”两朵乌云“：“第二朵乌云出现在关于能量均分的麦克斯韦-玻尔兹曼理论上”。第二朵乌云导致量子论的诞生，他有2个具体所指，一个是大家熟知的（光子气）黑体辐射，另一个是我们即将讨论的（声子气）固体比热。能均分定理将在讨论后者的低温热力学性质中失效。这两个例子有非常多类似之处。

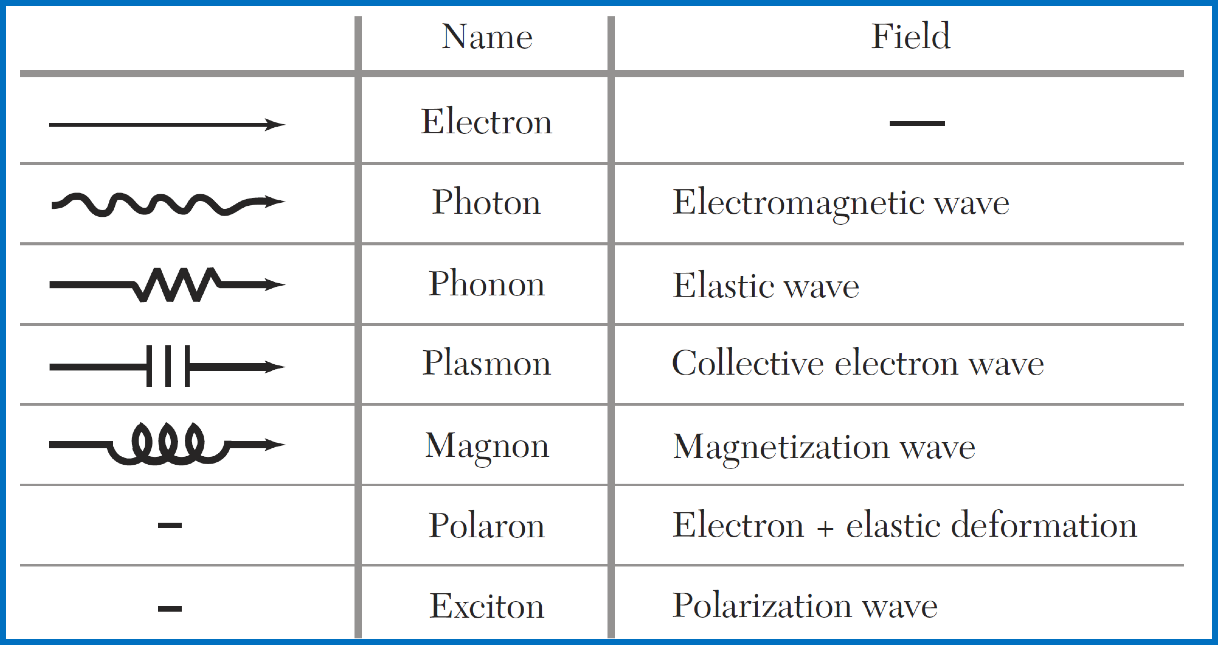
  量子场与准粒子

---

1. 一维原子链模型

• 三维晶格振动的纵波与横波（波矢K垂直原子面）

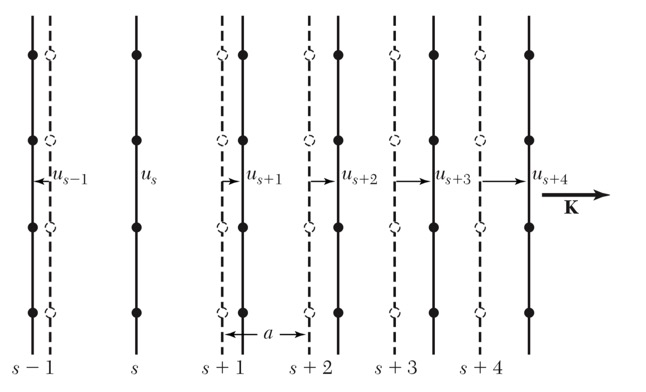
  三维晶格振动的纵波：原子运动平行于K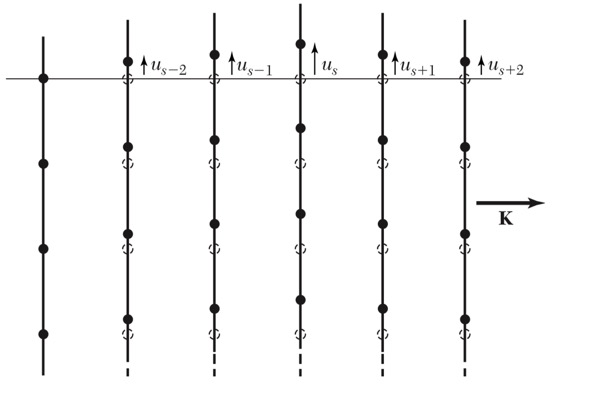
  横波振动：原子运动垂直于K

• 将晶格振动简化为下面的一维模型

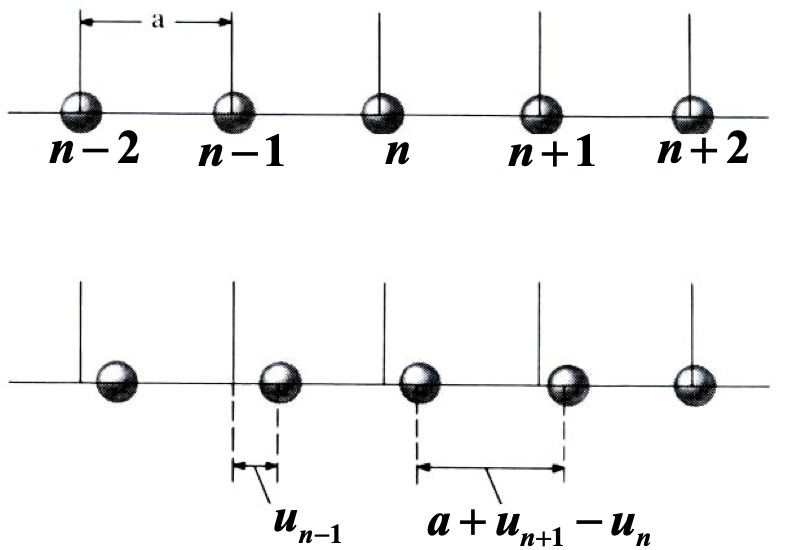
  一维原子链的耦合谐振子模型：（上图）原子处于平衡位置，晶格常数为$a$；（下图）偏离平衡位置的原子位形。假设第$n$个原子偏离平衡位置的矢量为$u_n$ ，在一维情况下$u_n$为一个可取正负值的标量，约定为向右为正，向左为负）。两个相邻原子$n$和$n+1$的间距为$u_{n+1}-u_n$。

• 简谐近似： 两个相邻原子间的相互作用势能为$\varphi (x)$，$x$为原子间距，固体中$x=a+\delta$，$\delta$为一小量。势能可以展开为：

  $\phi(a+\delta) = \phi(a) + \frac{d \phi(x)}{d x}|{x=a} \delta + \frac{1}{2!} \frac{d^2 \phi(x)}{d x^2}|{x=a} \delta^2 + …$

  由于$\varphi (a)$为势能极小点（不失一般性，取$\varphi (a)=0$），$\frac{d\varphi (x)}{dx}{|}_{x=a}=0$。

  按照简谐近似取到2阶项，并简记弹性系数$\beta \equiv \frac{d^2\varphi (x)}{d{x}^2}{|}_{x=a}$。

  • 弹性势能为：$\varphi (\delta )=\frac{1}{2}\beta {\delta }^2$

  • 弹性力为$f=-\frac{d\varphi }{d\delta }=-\beta \delta$

---

2. 格波

• 晶格振动运动方程与波动解

  $N$个相互耦合的谐振子，格波在其中传播。

  仅考虑最近邻相互作用，$N$个原子的耦合运动方程，对于第$n$个原子而言：

  $\beta (u_{n+1}-u_n)-\beta (u_n-u_{n-1})=M\frac{d{u}_n^2}{d{t}^2}$

  $M$为原子质量。

  • 为求解$N$个原子的耦合方程组，引入傅里叶变化，得到方程组的解为：

    $u_n(t)=A{e}^{i(qna-\omega t)}$，其中$A$为振幅，$\omega$为圆频率，$q$为波矢，是代表波的传播模式。

  • 代入运动方程，可以得到能动关系为：

    ${\omega }^2(q)=\frac{2\beta }{M}(1-\cos qa)$

    $\omega (q)=2\sqrt{\frac{\beta }{M}}|\sin \frac{qa}{2}|$

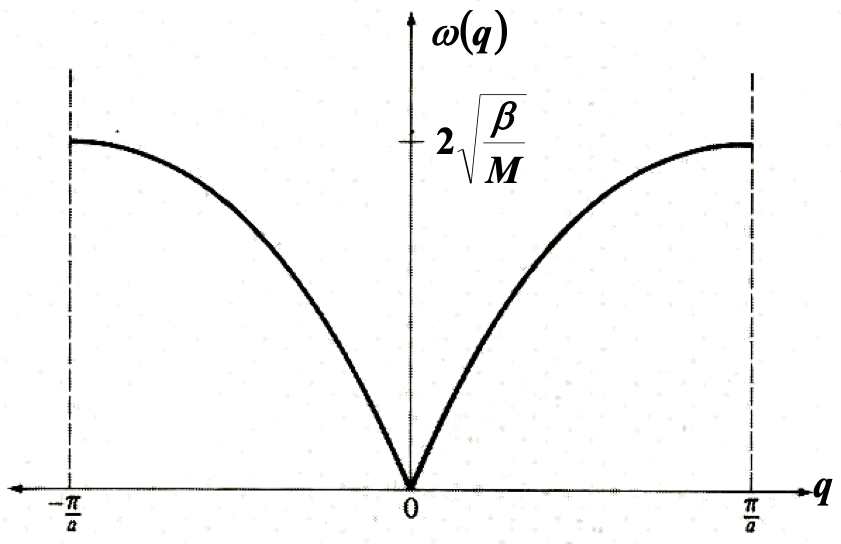
    一维原子链格波的 $\omega$ - $q$ 色散关系。

  • 长波极限： $q$趋近于0，$\omega (q)\simeq \sqrt{\frac{\beta }{M}}qa$，线性色散。

  • 在无穷长的热力学极限下，$q$可以连续的取值。但是为了方便处理，下面指出，有限尺寸系统的格波波矢$q$的取值有一定的要求。另外，在连续空间中，$q$可以从0取到无穷，但作为分立格点系统上的波矢$q$有一些特殊性。

• 波恩—冯卡曼边界条件

  为了处理问题方便，固体物理中常常采用具有周期边界条件的环（也称为波恩—冯卡曼边界条件），使得有限尺寸系统也具有了平移不变性和波数$q$。周期边界条件看似”不物理“，但是在热力学极限下（$N\to \mathrm{\infty }$），边界项对体态性质带来的影响不甚重要。

  周期边界条件对固体中许可的波矢提出了限制条件，即：

  $e^{iqna}=e^{iq(n+N)a}$，因此$qNa=2m\pi$

  因此波矢取一系列分立值，$q=m\frac{2\pi }{Na}$，$m$为整数。

• 等价波矢与布里渊区

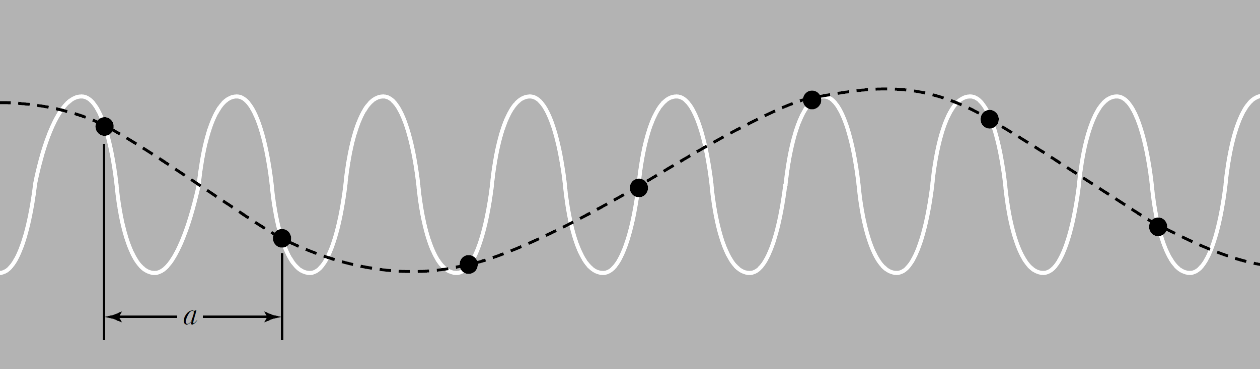
  上述两个格波波矢为 $q_1=\frac{2\pi }{5a}$（对应波长$\lambda =5a$）和波矢 $q_2=\frac{12\pi }{5a}$ （对应波长为$\frac{5}{6}a$），对于分立晶格系统，两个波矢 $q_1$ 和 $q_2$ 没有 区别。

  • 对于晶体系统，波矢 $q$ 与 $q+G$ 为等价波矢，其中 $G=m\frac{2\pi }{a}$ 为倒格矢。

    • 格点位移 $u_n=A{e}^{i(q+G)na}=A{e}^{iqna}$。
    • 色散关系 $\omega (q+G)=2\sqrt{\frac{\beta }{M}}|\sin (\frac{qa}{2}+\frac{Ga}{2})|=\omega (q)$

  • 考虑到原子位移和色散关系等晶格振动对 $q$ 的周期性，因此可以选取区间 $q\in [-\pi /a,\pi /a]$ 内的点来代表所有运动模式，称为布里渊区。

    • 在第一布里渊区内存在振动模式数目为 $\frac{2\pi /a}{2\pi /Na}=N$ ，与格点数目相等。无论是数实空间变量数目 $u_n$ 还是 $q$ 空间振动模式，总自由度不变。

    • 在布里渊区边界上 $q=\pm \pi /a$，$u_n=e^{iqna}=e^{in\pi }=(-1{)}^n$，代表正向与反向传播叠加的驻波解。

    • 按照入射波垂直晶面，$\theta =\pi /2$，布里渊区边界的点发生格波的布拉格反射。

      $2a\sin (\theta )=\lambda =2a$。

---

3. 双原子链：声学支与光学支

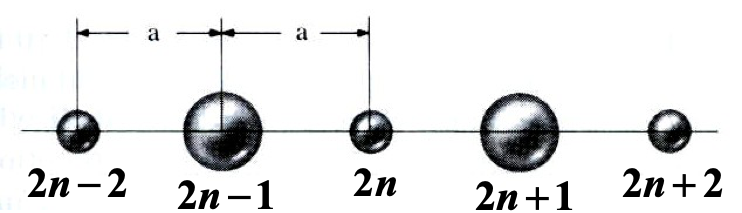双原子链系统，晶胞中包含两个不同质量的原子$M$和$m$，弹性系数为$\beta$，晶格常数为$2a$。

• 双原子链中，奇数格点上 $M$ 的位移标记为 $u_{2n-1},u_{2n+1},u_{2n+3},\dots$；而偶数格点上 $m$ 的位移标记为 $u_{2n-2},u_{2n},u_{2n+2},\dots$。

• 采取简谐近似，列出双原子链的$2N$个运动方程（Equation of Motion, EoM）

  $m\frac{d^2{u}_{2n}}{d{t}^2}=\beta (u_{2n+1}+u_{2n-1}-2u_{2n})$

  $m\frac{d^2{u}_{2n+1}}{d{t}^2}=\beta (u_{2n+2}+u_{2n}-2u_{2n+1})$

• 代入两个原子的位移波函数

  $u_{2n}=A{e}^{i[q(2n)a-\omega t]}$

  $u_{2n+1}=B{e}^{i[q(2n+1)a-\omega t]}$

  得到需要求解的方程组$X(A,B{)}^T=0$，其中$X$矩阵为

  $2\beta -m{\omega }^2$	$-2\beta \cos (qa)$
  $-2\beta \cos (qa)$	$2\beta -M{\omega }^2$

  令$|X|=0$，得到本征运动模式和色散关系如下：

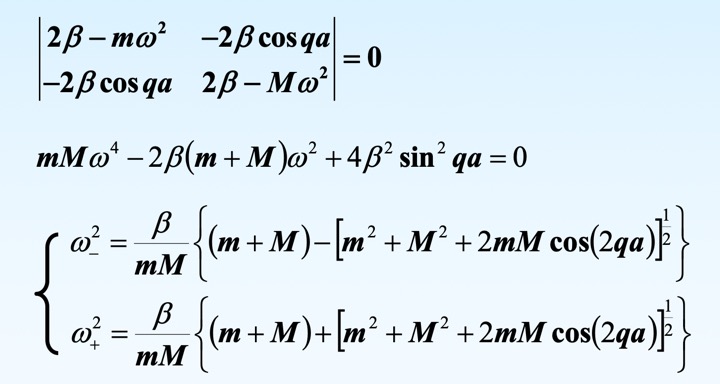
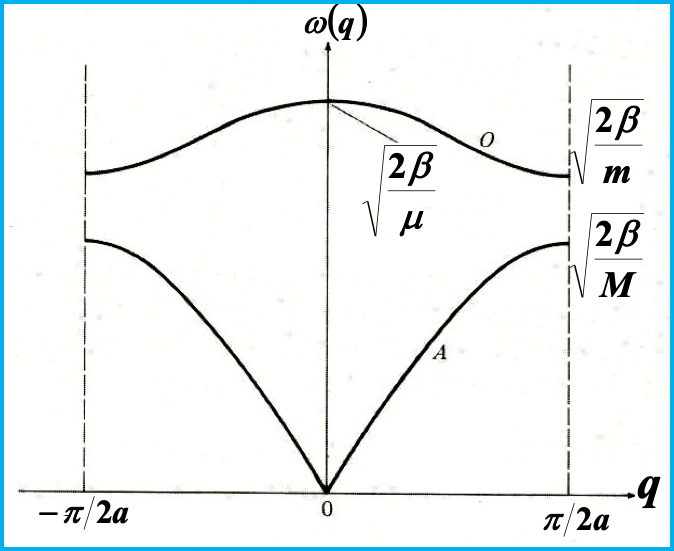
  久期方程	色散关系，存在两支解，分别称为光学支和声学支

• 布里渊区，振动模式数，等价 $q$ 点

  • 按照波恩-冯卡曼边界条件，第一布里渊区范围为：$q\in [-\frac{\pi }{2a},\frac{\pi }{2a}]$，波矢最小间距为 $\frac{2\pi }{2Na}$，每支激发上的 $q$ 点数目为 $(\frac{\pi }{a})/(\frac{\pi }{Na})=N$，两支激发共计 $2N$ 振动模式，与双原子链自由度吻合。

  • 按照 $G=\frac{2\pi }{2a}$，因为 $\cos [2(q+G)a]=\cos [2(q+\frac{\pi }{a})a]=\cos (2qa)$

    可以得到 ${\omega }_{\pm }(q+G)={\omega }_{\pm }(q)$。

• 长波极限

  取$q\to 0$的长波极限，对色散关系进行分析：

  声学支: 零能激发无能隙，线性色散。
  光学支：长波光学支激发能隙 $\sqrt{\frac{2\beta }{\mu }}$，$\mu =\frac{mM}{m+M}$

  • 长波声学支图像

    求解久期方程得到本征能量后，可以求得振幅$A,B$的比值

    $A/B=[2\beta -M{\omega }^2]/[2\beta \cos (qa)]$

    在长波声学支解中，取$q\to 0$（同时$\omega \to 0$）：

    $A/B\simeq 1$

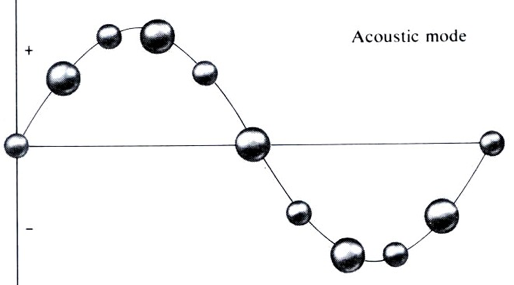
    双原子质心做类似单原子链运动

  • 长波光学支图像

    $A/B\simeq [2\beta -M\frac{2\beta }{mM}(M+m)]/2\beta =-\frac{m}{M}$

    因此光学支长波振动中质心不动：$AM+Bm=0$。

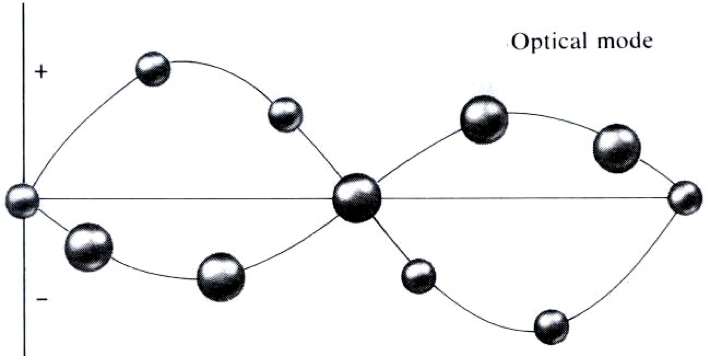
    双原子围绕质心振动，容易被电磁波激发

---

4. 简正模式与格波量子化

通过上面的讨论，我们知道晶格振动可以化为一系列正交归一完备的平面波的叠加。因此，我们可以把描述从实空间原子坐标$u_n$转换为广义坐标——波函数分量的振幅$A_q$。

• 第$n$个原子的位移$u_n$可以展开成

  $u_n=\sum _q{A}_q{e}^{i(qna-{\omega }_{q}t)}+A_q^{\ast }{e}^{-i(qna-{\omega }_{q}t)}=\frac{1}{\sqrt{N}}\sum _q{a}_q{e}^{iqna}+a_q^{\ast }{e}^{-iqna}$

  其中坐标 $a_q=\sqrt{N}{A}_a{e}^{-i{\omega }_{q}t},a_q^{\ast }=\sqrt{N}{A}_a^{\ast }{e}^{i{\omega }_{q}t}$。

• 格波的动能为

  $T=\frac{M}{2}\sum _{n=1}^N{\dot{u}}_n{\dot{u}}_n$

  将$u_n$用$a_q$表达，得到：

  $T=\frac{M}{2N}\sum _{n=1}^N(\sum _q{\dot{a}}_q{e}^{iqna}+{\dot{a}}_q^{\ast }{e}^{-iqna})(\sum _q{\dot{a}}_q{e}^{iqna}+{\dot{a}}_q^{\ast }{e}^{-iqna})$

  并考虑到${\dot{a}}_q=-i{\omega }_q{a}_q$

  $T=\frac{M}{2}\sum _q{\omega }_q^2(2a_q{a}_q^{\ast }-a_q{a}_{-q}-a_q^{\ast }{a}_{-q}^{\ast })$。

• 原子势能项为

  $V=\frac{\beta }{2}\sum _n(u_n-u_{n-1})(u_n-u_{n-1})=\frac{M}{2}\sum _q{\omega }_q^2(2a_q{a}_q^{\ast }+a_q{a}_{-q}+a_q^{\ast }{a}_{-q}^{\ast })$

  其中使用了 $\frac{\beta }{2}(2-e^{iqa}-e^{-iqa})=\beta [1-cos(qa)]=2\beta {\sin }^2\frac{qa}{2}=\frac{M}{2}{\omega }_q^2$

• 哈密顿量

  $H=T+V=M\sum _q{\omega }_q^2(a_q{a}_q^{\ast }+a_q^{\ast }{a}_q)$

• 引入（实）简正坐标 $x_q$与共轭动量$p_q$

  $x_q=a_q+a_q^{\ast }$

  $p_q=\frac{M{\omega }_q}{i}(a_q-a_q^{\ast })$

  其逆变换为

  $a_q=\frac{1}{2}(x_q+\frac{i}{M{\omega }_q}{p}_q)$

  $a_q^{\ast }=\frac{1}{2}(x_q-\frac{i}{M{\omega }_q}{p}_q)$

• 使用简正坐标，可以将哈密顿量表达为简正模式之和

  $H=\frac{M}{2}\sum _q{\omega }_q^2(x_q^2+\frac{1}{M^2{\omega }^2}{p}_q^2)=\sum _q\frac{M}{2}{\omega }_q^2{x}_q^2+\frac{p_q^2}{2M}$

• 简正模式量子化与声子

  系统的总哈密顿量 $H=\sum _q{H}_q$，其中$H_q=\frac{M}{2}{\omega }_q^2{x}_q^2+\frac{p_q^2}{2M}$，即解耦的谐振子——简正模式。

  量子化： 将每个简正模式$H_q$量子化，即量子谐振子。引入阶梯算符$a,a^{†}$，则谐振子可以写作

  $a_q=\sqrt{\frac{M\omega }{2\hslash }}(x_q+\frac{i}{M{\omega }_q}{p}_q)$

  $a_q^{†}=\sqrt{\frac{M\omega }{2\hslash }}(x_q-\frac{i}{M{\omega }_q}{p}_q)$

  验证$[a_q,a_{q^{\prime }}^{†}]={\delta }_{q,q^{\prime }}$

  $H_q=\hslash {\omega }_q{a}_q{a}_q^{†}=\hslash {\omega }_q(n_q+1/2)$，其中$n_q=a_q^{†}{a}_q$表示简正模式处在第$n_q$个激发态。

  声子： 简正模式${\omega }_q$处于第$n_q$个激发态则激发$n_q$个声子。则晶格振动可以表达为$q$-模式激发$n_q$个声子的集合（无相互作用声子气）。注意，$q$-模式所激发的声子不是某个原子的个别激发带来的，而是所有$N$个原子的集体激发。

---

5. 长波极限下的一维自由玻色场

上面介绍的是分立情况下的量子化过程。在有些情况下，先取连续极限，写成经典场然后将其做正则量子化的过程，推导更为简明、系统，下面介绍这部分内容。

• 先写下晶格振动的拉格朗日量：

  $L = T - V = \sum_{n=1}^{N} \frac{m \dot{u}n^2}{2} - \frac{\beta}{2} (u{n+1} - u_n)^2$

• 从凝聚态物理的现代视角，我们特别关心系统的低能激发，在晶格振动问题上，这对应着长波极限，因此我们取连续极限将分立$u_n$映射成经典连续场$\varphi (x)$，其中：

  $u_n\to a^{1/2}\varphi (x)$，其中$1/2$为标度维度(scaling dimension)

  $u_{n+1}-u_n\to a^{3/2}{\partial }_x\varphi$，标度维度为$3/2$

  $\sum _n\to \frac{1}{a}{\int }_0^{L}dx$，其中 $L=Na$

• 拉氏量：$L={\int }_0^L\mathcal{L}(\varphi ,{\partial }_x\varphi ,\dot{\varphi })dx$，其中 $\mathcal{L}(\varphi ,{\partial }_x\varphi ,\dot{\varphi })=\frac{m}{2}{\dot{\varphi }}^2-\frac{\beta a^2}{2}({\partial }_x\varphi {)}^2$ 为拉氏密度。

• 经典场论

  • 作用量$S[\varphi ]=\int dt\int dx\mathcal{L}(\varphi ,{\partial }_x\varphi ,\dot{\varphi })$

  • 作用量极小原理 $\delta S[\varphi ]=0$可以推导出拉式运动方程：

    ​ $\varphi (x,t)\to \varphi (x,t)+\eta (x,t)\cdot ϵ$

  • $\delta S=\int dt\int dx[\frac{m}{2}(\dot{\varphi }+ϵ\dot{\eta }{)}^2-\frac{\beta a^2}{2}({\partial }_x\varphi +ϵ{\partial }_x\eta {)}^2-\frac{m}{2}{\dot{\varphi }}^2+\frac{\beta a^2}{2}({\partial }_x\varphi {)}^2]$

  • 忽略${ϵ}^2$以上高阶项，可以得到：

    $\int dx\int dtϵ(m\dot{\varphi }\dot{\eta }-\beta a^2{\partial }_x\varphi {\partial }_x\eta )=0$

    分步积分，并假定$\eta (x,t)$在无穷远处（积分的上下界处）为0，即得：

    $m{\partial }_t^2\varphi -\beta a^2{\partial }_x^2\varphi =0$，场的拉氏运动方程（波动方程）。

  • 波动方程的一般解：${\varphi }_{\pm }(x\mp vt)$，代入运动方程不难得到：

    $m{v}^2{\partial }_t^2{\varphi }_{\pm }-\beta a^2{\partial }_x^2{\varphi }_{\pm }=0$

    即：$v=a\sqrt{\frac{\beta }{m}}$。

  • 不失一般性，可以选取平面波作为正交归一的基底展开任意波函数。

• 经典场论的哈密顿形式

  • 按照分析力学，引入正则动量 $\pi (x)=\frac{\partial \mathcal{L}(\varphi ,{\partial }_x\varphi ,\dot{\varphi })}{\partial \dot{\varphi }}=m\dot{\varphi }$

  • 泊松括号：{$\pi (x),\varphi (x^{\prime })$} $=-\delta (x-x^{\prime })$

  • 哈密顿密度：$\mathcal{H}(\pi ,{\partial }_x\varphi ,\dot{\varphi })=\pi \dot{\varphi }-\mathcal{L}(\varphi ,{\partial }_x\varphi ,\dot{\varphi })=\frac{{\pi }^2}{2m}+\frac{\beta a^2}{2}({\partial }_x\varphi {)}^2$

  • 哈密顿量可以写成哈密顿密度的积分

    $H[\pi ,\varphi ]=\int dx\mathcal{H}=\int dx[\frac{{\pi }^2}{2m}+\frac{\beta a^2}{2}({\partial }_x\varphi {)}^2]$

• 场量子化

  • 提升$\pi (x)$和$\varphi (x)$为场算符$\hat{\pi }(x),\hat{\varphi }(x)$，满足$[\hat{\pi }(x),\hat{\varphi }(x^{\prime })]=-i\hslash \delta (x-x^{\prime })$。

  • 傅里叶变换到动量空场算符${\pi }_k,{\varphi }_k$

    ${\pi }_k=\frac{1}{\sqrt{L}}{\int }_0^{L}dx{e}^{ikx}\pi (x)$

    ${\varphi }_k=\frac{1}{\sqrt{L}}{\int }_0^{L}dx{e}^{-ikx}\varphi (x)$

  • 验证关系：${\pi }_{-k}={\pi }_k^{†}$ （已知$\pi (x{)}^{†}=\pi (x)$）。

  • 量子哈密顿量可以写成简正模式的和

    $H=\int dx\mathcal{H}=\int dx\frac{1}{2mL}(\sum _k{e}^{-ikx}{\pi }_k{)}^2+\frac{\beta a^2}{2L}(\sum _{k}ik{e}^{ikx}{\varphi }_k{)}^2$

    ​ $=\sum _k(\frac{1}{2m}{\pi }_k{\pi }_{-k}+\frac{\beta a^2{k}^2}{2}{\varphi }_k{\varphi }_{-k})$

    ​ $=\sum _k(\frac{1}{2m}{\pi }_k{\pi }_{-k}+\frac{m{\omega }_k^2}{2}{\varphi }_k{\varphi }_{-k})$

    其中${\omega }_k=vk$，$v=\sqrt{\frac{\beta a^2}{2m}}$为波速

    如果将${\pi }_{-k}{\pi }_k$ 视为$|{\pi }_k{|}^2$，${\varphi }_k{\varphi }_{-k}$视为$|{\varphi }_k{|}^2$，则量子哈密顿量非常类似于一个谐振子。

• 引入场的产生消灭算符

  $a_k=\sqrt{\frac{m{\omega }_k}{2\hslash }}({\varphi }_k+\frac{i}{m{\omega }_k}{\pi }_{-k})$

  $a_k^{†}=\sqrt{\frac{m{\omega }_k}{2\hslash }}({\varphi }_{-k}-\frac{i}{m{\omega }_k}{\pi }_k)$

  作业：验证 $[a_k,a_k^{†}]=1$

  $a_k^{†}$ 表示产生一个$k$-模式玻色子的产生算符，$a_k$表示消灭算符，$n_k=a_k^{†}{a}_k$表示$k$-模式的粒子数。

  将哈密顿量写成对角形式

  $H=\sum _k\hslash {\omega }_k(a_k^{†}{a}_k+\frac{1}{2})$。

• 比较声子的两种导出方式（1）分立格点推导的优势在于直观、简单、具有启发性，但缺点在于推导过程不够一般；（2）先取连续极限，然后正则量子化的做法系统、规范、具有普适性。

---

Slides & Video

• Slides for Chapter 3 can be downloaded

  

• Video lectures (two, by Sandro Scandolo, ICTP), please click the icon below.

  • Lecture 19
  • Lecture 20

Discussions

• An online discussion (c.a. 90 min, via Wechat or Dingtalk) will be arranged.

Homework

1. 长波极限下的运动方程：对于简单原子链，请证明在长波极限下运动方程可以化为连续介质波动方程

   $\frac{d^{2}u}{d{t}^2}=v^2\frac{d^{2}u}{d{x}^2}$，其中$v$为弹性波的波速。

2. 考虑一个两周期原子链，耦合弹性系数按照${\beta }_1$和${\beta }_2$交替，写出原子链的运动方程，并求解本征运动模式和本征能量。

3. 验证算符对易子：

   （1）从 $[\pi (x),\varphi (x^{\prime })]=-i\hslash \delta (x-x^{\prime })$，导出$[{\pi }_k,{\varphi }_{k^{\prime }}]=-i\hslash {\delta }_{k,k^{\prime }}$;

   （2）继续导出$[a_k,a_{k^{\prime }}^{†}]={\delta }_{k,k^{\prime }}$，玻色子对易关系。

[assigned: 30-March-2020, due: 06-April-2020]